【高校数学でわかる】コロナウイルスPCR検査の限界

「海外では，ドライブスルー方式で検査をしている国もあるのになぜ，日本はしないの？」「全国民にPCR検査をしたら，陰性の人は普通の生活ができるんじゃないの？」

コロナウイルスのPCR検査についてこんな疑問を抱えている人も多いかと思います．しかし，PCR検査をしても，陰性の人が実際には感染者である可能性を否定できません．

これは，現在の日本の状況では，PCR検査で感染者を見つけられる確率が低いことと関係してきます．

今日は，PCR検査で感染者を見つけることがなぜ難しいのかを，高校数学Aの知識でわかるように説明していきます．

　条件付き確率とベイズの定理

まず，条件付き確率の復習をしましょう．

• 事象Aが発生する確率を，\(P(A)\)
• 事象A，事象Xがどちらも発生する確率を，\(P(A\cap X)\)
• 事象Xが発生したもとで，事象Aが発生する条件付き確率を，\(P(A|X)\)
• この時，\(P(A|X)\)は，以下のように定義されます．
  $$P(A|X) = \frac{P(A\cap X)}{P(X)} \tag{1}$$
  $$P(A\cap X) = P(A|X)P(X) \tag{2}$$

• ここで，\(P(A\cap X) = P(X\cap A)\)と式(2)より
  $$P(A|X)P(X) = P(X|A)P(A) \tag{3}$$
• 式(1)および式(3)より，次の式が導出されます．（統計学ではベイズの定理と呼ばれています．）
  $$P(A|X) = \frac{P(X|A)P(A)}{P(X)} \tag{4}$$

　PCR検査の限界

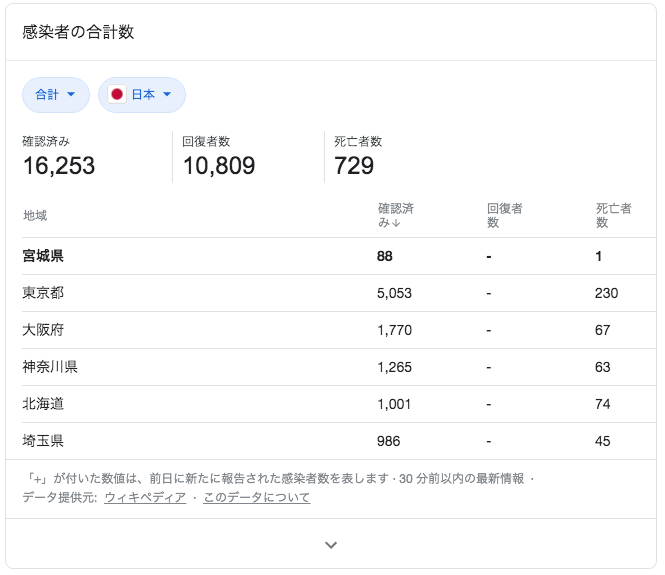
まずは，感染率を求めるために，現在の累計感染者数をgoogle先生に聞いてみます．
2020年5月17日19時29分，日本国内の感染者数は16253人でした．続いて日本の総人口は，1億2650万人です．

PCR検査の正確性（感度，特異度）は公表されていませんが，ここでは，SARSの数値を参考にします．
Richardson SE, Tellier R & Mahony J (2004) によれば，SARSの場合，発症後数日以内であれば感度は80％程度，特異度は多くの研究で90％以上とされているようです．（アブストラクトしか読んでいないので．もし間違えていたら教えてください．）
これをもとに以下のように設定します．

それでは，ベイズの定理よりコロナウイルスPCR検査の限界について考えていきます．まずは，以下のように確率を定義します．

この時，PCR検査で陽性の判定を受けた人が，実際に感染者である確率\(P(感染|陽性)\)を求めてみます．これは，ベイズの定理 (4)より以下の式で表されます．
$$P(感染|陽性) = \frac{P(陽性|感染)P(感染)}{P(陽性)} \tag{5}$$

ここで，陽性率\(P(陽性)\)の値は，感度と特異度，感染率をもとに算出できます．陽性の判定を受けるには2パターンあります．

• 一つ目は，感染者に対して正しく陽性と判定：\(感度 \times P(感染)\)
• 二つ目は，非感染者に対して誤って陽性と判定：\((1-特異度) \times P(非感染) \)

よって，陽性率\(P(陽性)\)の値はこれらを足し合わせれば良いですから，
$$P(陽性) = 0.80 \times 0.000128 + (1-0.95) \times 0.999872 \approx 0.0500 = 5\% \tag{6}$$
（この5％の陽性率に関しては，あとのセクションで検証します．）

さらに，感染がわかっている人がPCR検査で陽性の判定を受ける確率\(P(陽性|感染)\)は，感度のことを意味していますので，式(5)および式(6)から\(P(感染|陽性)\)が求まります．

まさ

PCR検査で陽性とわかった人が，本当に感染者である確率がこんなに低いなんて．．．

しかし，どうしてこの問題設定で2％という低い数字が出たのでしょうか？
次のページでは，どうやったらPCR検査で陽性の人が実際に感染者である確率をあげられるのか，考えていきます．

まさ

エキゾテクブログの管理人。
現在は、フトアゴヒゲトカゲ2匹、マリトゲオアガマ、コモンフラットロックリザードを飼育中。