なぜPCR検査で感染者を見つけるのは難しいのか？
先ほどの問題設定で，PCR検査で感染者を見つけるのが相当難しいことがわかりました．ではなぜ，陽性の判定を受けた人でも感染者である確率がこんなに低いのでしょうか？
その答えは，日本人の多くがコロナウイルスに感染していないからと言えます．
これを説明するために，感染率\(P(感染)\)の値を大きくして考えてみます．ここでは，
- $$P(感染) = 0.50 = 50\%$$
とします．考えたくもないですがこれは，日本人の50％がコロナウイルスに感染した状況を意味します．この時，
陽性の判定を受けた人が感染者である確率が94%まで上がった！
つまり，PCR検査で感染者を効率よく発見できるのは，日本人の多くがコロナウイルスに感染した状況下である．と言えます．
しかし日本には，優秀な専門家を集めて，この問題に立ち向かった経緯があります．
そう，クラスター対策です．
なぜクラスター対策が優秀と言えるのか？
ここまでで，PCR検査で感染者を見つけるためには，高い感染率が必要であることがおわかりいただけたと思います．
実は，この感染率を高める戦略こそ，「クラスター対策」なのです．
クラスター対策は，PCR検査をクラスターが発生した集団に限定して行うという戦略でした．
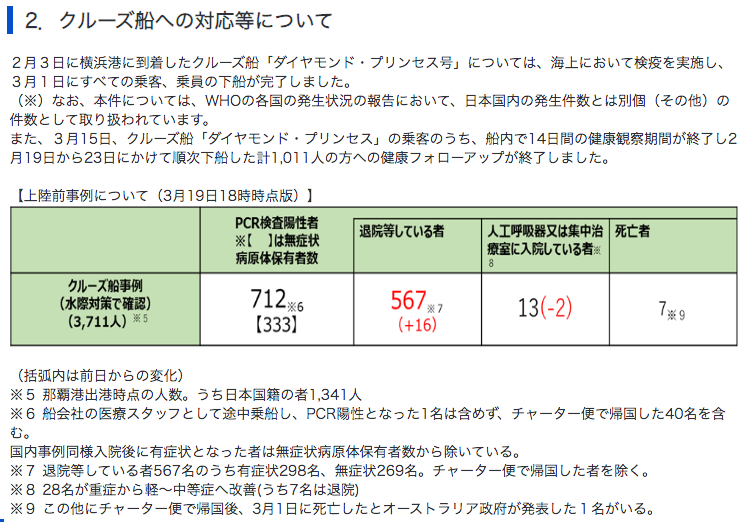
感染率はクラスター内部に限定すれば非常に高い数値となります．例として日本国内で発生した最も大きなクラスター「ダイヤモンドプリンセス号」を例に説明します．
ダイヤモンドプリンセス号では，乗客3711人のうち，712人がコロナウイルスに感染したとされています．つまり，感染率\(P(感染) = \frac{712}{3711} \approx 0.192 = 19.2\%\)
さて，この時陽性の判定を受けた人が実際に感染者である確率はどうなるでしょうか？
クラスター対策の効果がよくわかるね！
クラスター対策によって，陽性の判定を受けた人が実際に感染者である確率が2％から72％にまで向上することがわかりました．
さて，ここまで，長々と見ていただき本当にありがとうございます．
最後に，放置してきたPCR検査陽性率について検証していきます．
東京都が公表した陽性率
2020年5月8日，東京都が初めて，PCR検査の陽性率を公表しました．
「東京都は８日から、都内で行われた新型コロナウイルスのＰＣＲ検査について、独自の方法で算出した数字を「陽性率」として公表することになりました。
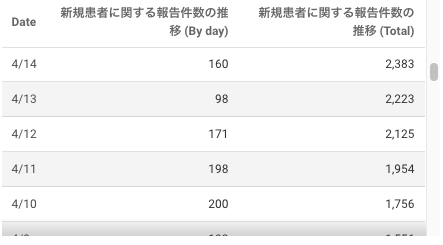
それによりますと、ピークは４月11日と14日で、いずれも31.6％でした。その後、減少する傾向が続き７日は7.5％でした。」
これによると，陽性率はピーク時で31.6%だったようです．また，以下より4月14日時点における東京都の累計感染者数は2383人とわかります．
東京都の人口は，927.3万人とされていますから，感染率\(P(感染) = \frac{2383}{9273000} \approx 0.000257 = 0.0257\%\)
これらから，感度と特異度を推定します．式(6)を参考にして，
$$P(陽性) = 感度 \times 0.000257 + (1-特異度) \times (1-0.000257) \approx 0.316 = 31.6\%$$
変数が2つあるので，難しいですね．
ここでは，感度95.0％，特異度96.9％にしてみたら，陽性率31.2%と実際に近い値が得られたので，参考までにこの数値を利用することにします．
（計算してみて思ったのですが，このデータからは，感度，特異度ともに100％に近い数値が必要でした．日本のPCR検査の正確性は極めて高いのかもしれません．）
PCR検査で陽性の判定を受けても，実際に感染している確率は0.7%！？
なぜ，こうなるのか？感染率\(P(感染)\)が極めて低いからです．
クラスターに対して，PCR検査を施していた時には，感染率が高いためにPCR検査の信頼度が高かったです．
やはり，PCR検査の規模を広げても，感染率が余計に低くなるだけですから意味がないのではないでしょうか？
日本国民全員にPCR検査を施すなどもってのほかです．
まとめ
PCR検査は正確性がいくら高くとも，使い方次第で全くもって意味のない検査になってしまうのです．
また，何度も触れましたが，早期のクラスター対策がコロナウイルス感染拡大に一役買ったことはまちがいないのではないでしょうか？
今回は触れませんでしたが，似たような計算方法で，PCR検査は再検査をすることで陽性者が実際に感染している確率をあげることができることも示せます．
これについても，そのうち記事にしようと思います．
エキゾテクブログの管理人。
現在は、フトアゴヒゲトカゲ2匹、マリトゲオアガマ、コモンフラットロックリザードを飼育中。
コメント
まじかよと思って三回くらい見直してしまいました
そもそも感染率のめちゃめちゃ低い母集団を検査する意味がないってことなんですね わかりやすくてすごい
次も読むからがんばって書いてね
コメントいただきありがとうございます！
自分でも計算結果が信じられずに，年度も計算し直しました笑
次もがんばって書きます！